|
EN BREF
|
Calculer le volume d’un prisme peut sembler complexe, mais il s’agit en réalité d’un processus simple qui repose sur quelques notions fondamentales de géométrie. Que ce soit pour un prisme à base rectangulaire, triangulaire ou hexagonale, la méthode reste similaire : il faut multiplier l’aire de la base par la hauteur du prisme. Dans ce guide complet, nous allons explorer les étapes nécessaires pour déterminer ce volume, illustrer les formules appropriées et fournir des exemples concrets afin que chacun puisse maîtriser ce concept essentiel en mathématiques.
Calculer le volume d’un prisme est une notion fondamentale en mathématiques, particulièrement dans le domaine de la géométrie. Ce guide vous accompagnera à travers les étapes nécessaires pour déterminer le volume de différents types de prismes, en expliquant les formules à utiliser et les concepts clés qui les sous-tendent. Que vous soyez débutant ou que vous souhaitiez approfondir vos connaissances, ce contenu est conçu pour rendre l’apprentissage accessible et compréhensible.
Qu’est-ce qu’un prisme ?
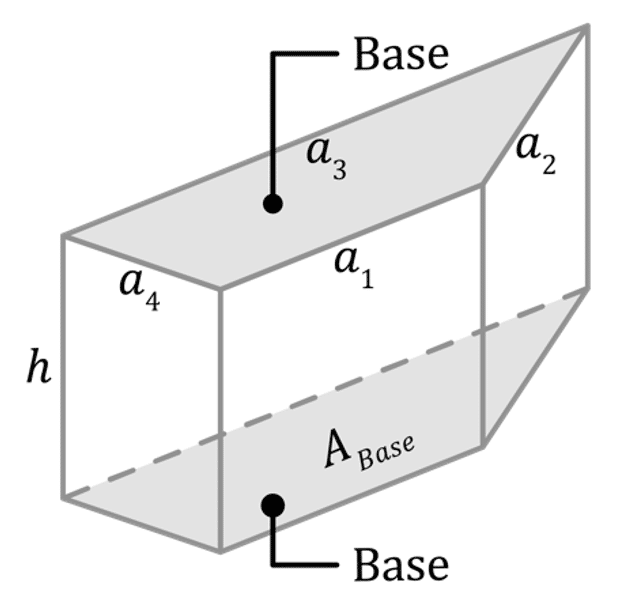
Un prisme est un solide géométrique qui se compose de deux bases parallèles et de faces latérales qui sont des parallélogrammes. Les bases peuvent être de différentes formes, comme des triangles, des rectangles ou des hexagones. La hauteur du prisme est la distance perpendiculaire entre les deux bases. La valeur du volume de ce solide dépend donc de l’aire de sa base et de sa hauteur.
La formule du volume d’un prisme
La formule générale pour calculer le volume d’un prisme est :
V = A * h
Dans cette équation, V représente le volume, A l’aire de la base et h la hauteur du prisme. Cette formule est simple mais fondamentale pour le calcul du volume, quel que soit le type de prisme.
Calculer l’aire de la base
Avant de pouvoir déterminer le volume d’un prisme, il est nécessaire de calculer l’aire de sa base. Selon la forme de la base, les méthodes de calcul varient :
Base rectangulaire
Pour un prisme à base rectangulaire, l’aire est déterminée par la formule :
A = L * l
où L est la longueur et l la largeur du rectangle.
Base triangulaire
Pour un prisme ayant une base triangulaire, l’aire se calcule ainsi :
A = (b * h) / 2
où b est la base du triangle et h sa hauteur.
Base hexagonale
Enfin, pour une base hexagonale, l’aire peut être trouvée avec la formule :
A = (3 * racine(3) * s²) / 2
où s est la longueur d’un côté de l’hexagone.
Calcul du volume d’un prisme
Une fois que vous avez déterminé l’aire de la base, le calcul du volume est rapide. Multipliez simplement l’aire de la base par la hauteur du prisme.
Exemple de calcul
Par exemple, si un prisme a une base rectangulaire de 3 m de long et 2 m de large, et une hauteur de 4 m, le calcul serait :
Aire de la base = 3 m * 2 m = 6 m²
Volume = 6 m² * 4 m = 24 m³
Ainsi, le volume du prisme est de 24 mètres cubes.
Applications et importance
Le calcul des volumes est essentiel dans divers domaines tels que l’architecture, l’ingénierie et les sciences naturelles. Comprendre comment évaluer le volume d’un prisme permet d’appréhender des concepts plus complexes et d’appliquer ces connaissances à des problèmes pratiques.
En somme, maîtriser le calcul du volume des prismes est une compétence clé en mathématiques. En connaissant la formule et en sachant comment calculer l’aire de la base, vous pouvez facilement déterminer le volume de n’importe quel prisme. La pratique régulière et l’application de ces concepts vous aideront à consolider vos compétences en géométrie.
| Étapes | Détails |
| 1. Identifier la base | Déterminez la forme de la base (carrée, rectangulaire, triangulaire, etc.). |
| 2. Calculer l’aire de la base | Utilisez la formule appropriée pour obtenir l’aire (ex: A = b × h pour un rectangle). |
| 3. Mesurer la hauteur | Mesurez la distance perpendiculaire entre les bases du prisme. |
| 4. Appliquer la formule | Multipliez l’aire de la base par la hauteur : V = A × h. |
| 5. Unité de volume | Exprimez le volume dans une unité cubique (ex: m³). |
Le volume d’un prisme est une mesure essentielle en géométrie qui indique la quantité d’espace à l’intérieur du solide. Pour le calculer, il suffit de multiplier l’aire de la base par la hauteur du prisme. Ce guide complet vous aidera à comprendre les étapes nécessaires pour effectuer ce calcul, ainsi que les formules à utiliser en fonction de la forme de la base du prisme.
Comprendre le volume d’un prisme
Le volume est une mesure tridimensionnelle qui quantifie l’espace occupé par un solide. Dans le cas des prismes, celui-ci est surtout déterminé par deux paramètres : l’aire de la base (A) et la hauteur (h) du prisme. Cette compréhension est cruciale avant d’appliquer les formules de calcul appropriées.
Formule du volume d’un prisme droit
Pour les prismes droits, la formule du volume est donnée par :
V = A × h
où V représente le volume, A est l’aire de la base, et h est la hauteur du prisme. Il suffit donc de multiplier l’aire de la base par la hauteur pour obtenir le volume souhaité.
Calcul de l’aire de la base
Avant de déterminer le volume, il est nécessaire de connaître l’aire de la base. Selon la forme de la base (rectangulaire, triangulaire, hexagonale, etc.), les calculs varient :
Aire d’une base rectangulaire
Pour un prisme à base rectangulaire, l’aire est calculée en multipliant la longueur par la largeur :
A = longueur × largeur
Aire d’une base triangulaire
Pour un prisme à base triangulaire, l’aire se calcule en utilisant la formule suivante :
A = (base × hauteur) / 2
Aire d’une base hexagonale
Pour une base hexagonale, l’aire est un peu plus complexe et peut être calculée avec :
A = (3√3 × côté²) / 2
Calcul du volume étape par étape
Suivez ces étapes pour calculer le volume d’un prisme :
- Trouvez l’aire de la base en utilisant la formule appropriée pour la forme de la base.
- Mesurez la hauteur du prisme.
- Multipliez l’aire de la base par la hauteur pour obtenir le volume.
Exemple de calcul
Imaginons un prisme à base triangulaire avec une base de 5 cm et une hauteur de 4 cm. Si la hauteur du prisme est de 10 cm, voici comment procéder :
Aire de la base = (5 × 4) / 2 = 10 cm²
Volume = A × h = 10 cm² × 10 cm = 100 cm³
Ainsi, le volume du prisme est de 100 cm³. Cet exemple illustre l’utilisation pratique des formules précédemment énoncées.
- Étape 1 : Identifier la base du prisme
- Étape 2 : Calculer l’aire de la base
- Étape 3 : Mesurer la hauteur du prisme
- Étape 4 : Appliquer la formule : V = A × h
- Étape 5 : Interpréter le résultat obtenu
Introduction au calcul du volume d’un prisme
Le volume d’un prisme est une mesure essentielle qui permet d’évaluer l’espace qu’occupe ce solide dans l’espace tridimensionnel. Dans cet article, nous allons explorer comment calculer le volume d’un prisme, en expliquant la méthode à suivre et en fournissant des exemples pratiques. Que vous soyez élève ou simplement curieux, ce guide vous permettra d’appréhender facilement cette notion fondamentale en géométrie.
Définition d’un prisme
Un prisme est un solide géométrique doté de deux bases parallèles et congruentes, et de faces latérales qui sont des parallélogrammes. Les bases peuvent avoir différentes formes, notamment triangulaires, carrées ou rectangulaires. La hauteur d’un prisme est la distance perpendiculaire entre les deux bases.
Formule générale pour le volume d’un prisme
Pour calculer le volume d’un prisme, on utilise la formule suivante :
V = Ab × h
Dans cette formule, V représente le volume, Ab est l’aire de la base du prisme et h est la hauteur. Cela signifie que le volume est obtenu en multipliant l’aire de la base par la hauteur du prisme.
Calculer l’aire de la base
Avant de pouvoir utiliser la formule du volume, il est essentiel de déterminer l’aire de la base du prisme. L’aire dépend de la forme de la base, qui peut être rectangulaire, triangulaire ou encore hexagonale. Voici quelques formules pour calculer l’aire en fonction de la forme de la base :
- Pour un prisme à base rectangulaire : Ab = longueur × largeur
- Pour un prisme à base triangulaire : Ab = (base × hauteur) / 2
- Pour un prisme à base hexagonale : Ab = (3 × racine carrée(3) / 2) × côté2
Application de la formule pour des prismes spécifiques
Exemple d’un prisme rectangulaire
Considérons un prisme rectangulaire dont la longueur est de 2 mètres, la largeur est de 1,5 mètre et la hauteur est de 3 mètres. Pour commencer, nous calculons l’aire de la base :
Ab = 2 × 1,5 = 3 m2
Ensuite, nous appliquons la formule pour déterminer le volume :
V = 3 × 3 = 9 m3
Exemple d’un prisme triangulaire
Prenons maintenant le cas d’un prisme à base triangulaire dont la base mesure 4 mètres, la hauteur du triangle 3 mètres et la hauteur du prisme est de 5 mètres. Premièrement, nous calculons l’aire de la base triangulaire :
Ab = (4 × 3) / 2 = 6 m2
Nous utilisons ensuite cette aire pour calculer le volume :
V = 6 × 5 = 30 m3
Conclusion temporaire
Connaître la méthode de calcul pour le volume d’un prisme est crucial, que ce soit pour des applications scolaires ou dans le monde professionnel. Avec la bonne compréhension des formes de base et l’utilisation de la formule appropriée, le calcul devient une tâche accessible à tous. N’hésitez pas à pratiquer avec différents types de prismes pour renforcer vos compétences mathématiques.